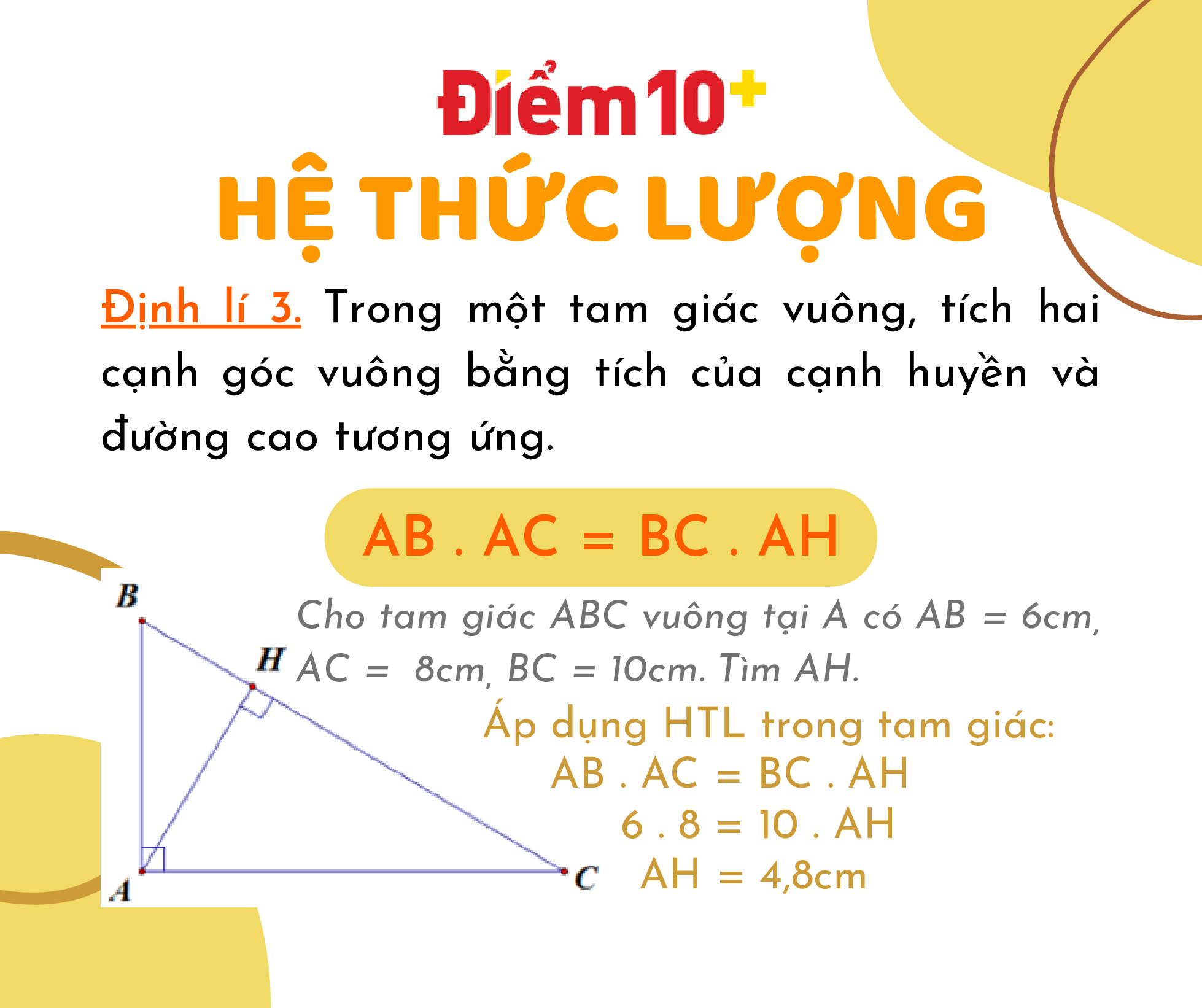
Hệ thức lượng trong tam giác vuông là một phần quan trọng của hình học, đặc biệt là trong việc giải các bài toán liên quan đến tam giác vuông. Những hệ thức này không chỉ giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các cạnh và góc trong tam giác vuông mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau như trắc địa, kiến trúc, và thậm chí là trong đời sống hàng ngày.

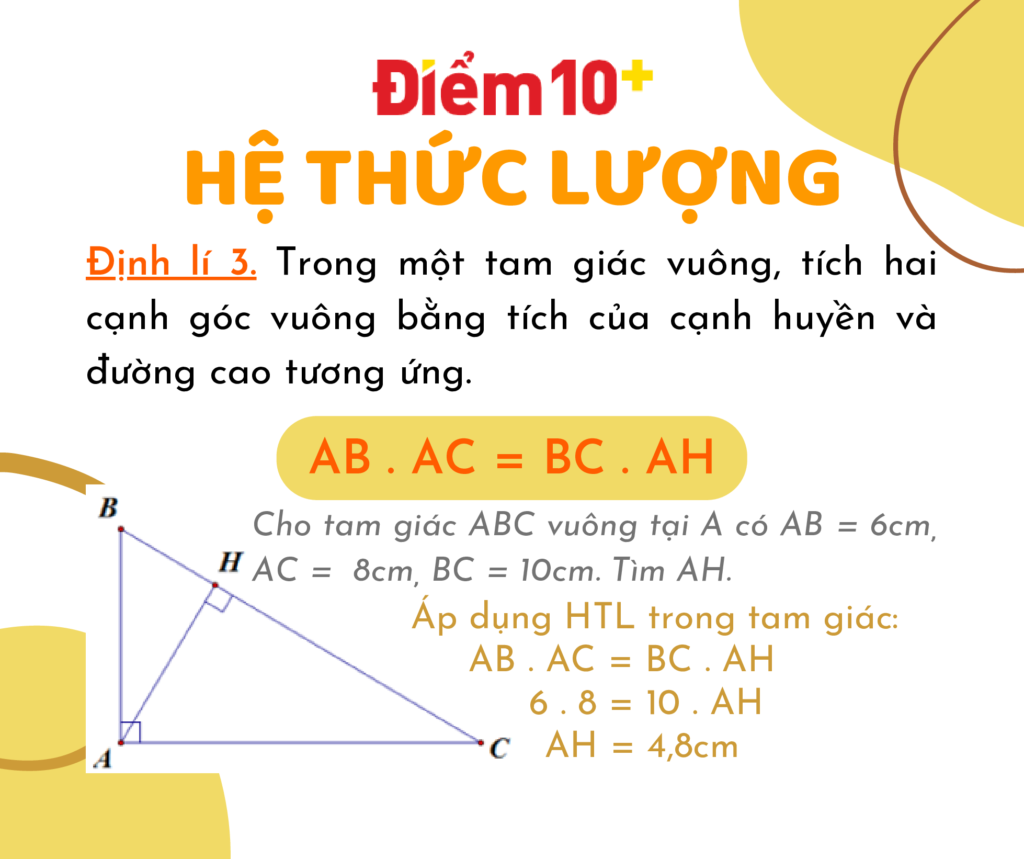
1. Định nghĩa và các khái niệm cơ bản

Tam giác vuông là tam giác có một góc vuông (90 độ). Trong tam giác vuông, cạnh đối diện với góc vuông được gọi là cạnh huyền, và hai cạnh còn lại được gọi là cạnh góc vuông. Các hệ thức lượng trong tam giác vuông bao gồm các công thức liên quan đến cạnh và góc của tam giác này.

2. Định lý Pythagore

Định lý Pythagore là một trong những hệ thức lượng cơ bản và quan trọng nhất trong tam giác vuông. Định lý này phát biểu rằng trong một tam giác vuông, bình phương độ dài của cạnh huyền bằng tổng bình phương độ dài của hai cạnh góc vuông. Công thức của định lý Pythagore là:

c^2 = a^2 + b^2c2=a2+b2

Trong đó:

• ( c ) là độ dài cạnh huyền
• ( a ) và ( b ) là độ dài hai cạnh góc vuông

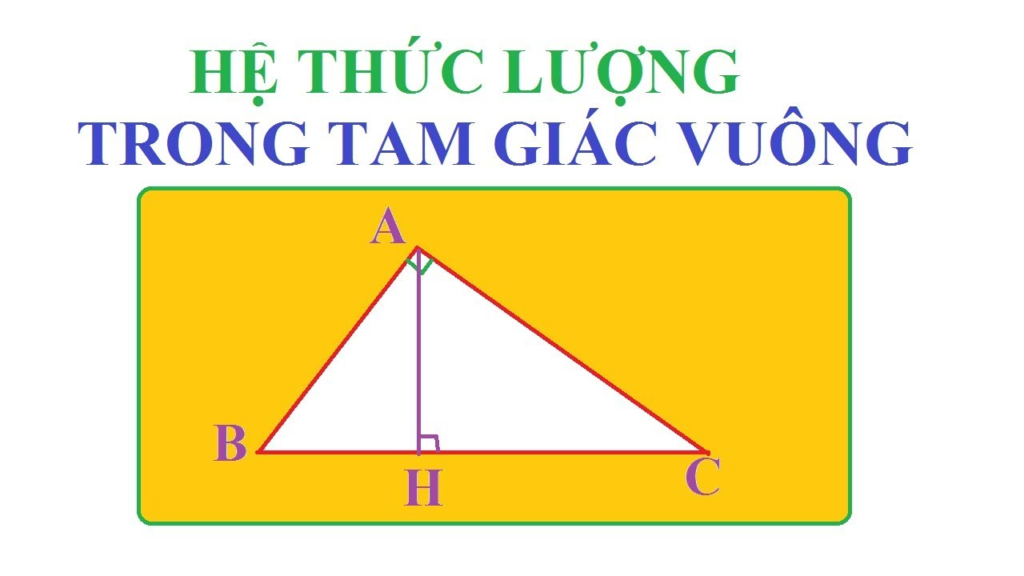
3. Các hệ thức lượng khác

Ngoài định lý Pythagore, còn có nhiều hệ thức lượng khác trong tam giác vuông, bao gồm:

• Hệ thức lượng về tỉ số lượng giác: Các tỉ số lượng giác như sin, cos, tan và cot của một góc trong tam giác vuông có thể được biểu diễn qua các cạnh của tam giác. Ví dụ:

\sin(\theta) = \frac{đối}{huyền}sin(θ)=huye^ˋnđo^ˊi​

\cos(\theta) = \frac{kề}{huyền}cos(θ)=huye^ˋnke^ˋ​

\tan(\theta) = \frac{đối}{kề}tan(θ)=ke^ˋđo^ˊi​

\cot(\theta) = \frac{kề}{đối}cot(θ)=đo^ˊike^ˋ​

• Hệ thức lượng về diện tích: Diện tích của một tam giác vuông có thể được tính bằng cách sử dụng hai cạnh góc vuông:

S = \frac{1}{2} \times a \times bS=21​×a×b

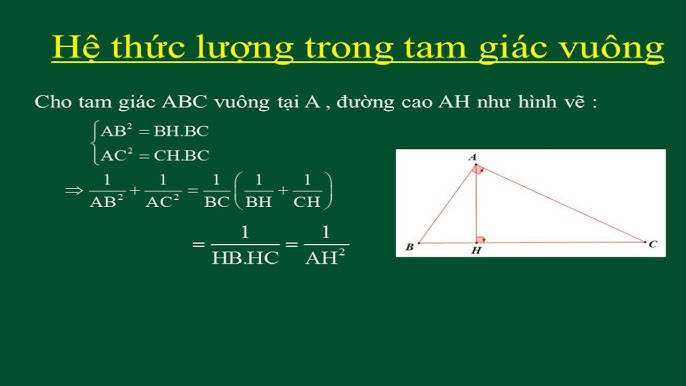
4. Ứng dụng của hệ thức lượng trong thực tế

Hệ thức lượng trong tam giác vuông có nhiều ứng dụng thực tế. Ví dụ, trong trắc địa, các kỹ sư sử dụng các hệ thức này để tính toán khoảng cách và độ cao. Trong kiến trúc, các hệ thức lượng giúp xác định các kích thước và góc của các cấu trúc xây dựng.

5. Một số bài toán ví dụ

Bài toán 1: Cho tam giác vuông ABC với góc vuông tại A, biết AB = 3 cm và AC = 4 cm. Tính độ dài cạnh BC.

Giải: Sử dụng định lý Pythagore:

BC^2 = AB^2 + AC^2BC2=AB2+AC2

BC^2 = 3^2 + 4^2BC2=32+42

BC^2 = 9 + 16BC2=9+16

BC^2 = 25BC2=25

BC = \sqrt{25} = 5 \text{ cm}BC=25​=5 cm

Bài toán 2: Cho tam giác vuông DEF với góc vuông tại D, biết DE = 5 cm và góc E = 30 độ. Tính độ dài cạnh DF và EF.

Giải: Sử dụng tỉ số lượng giác:

\sin(30^\circ) = \frac{DF}{DE}sin(30∘)=DEDF​

\frac{1}{2} = \frac{DF}{5}21​=5DF​

DF = \frac{5}{2} = 2.5 \text{ cm}DF=25​=2.5 cm

\cos(30^\circ) = \frac{EF}{DE}cos(30∘)=DEEF​

\frac{\sqrt{3}}{2} = \frac{EF}{5}23​​=5EF​

EF = 5 \times \frac{\sqrt{3}}{2} = 2.5\sqrt{3} \text{ cm}EF=5×23​​=2.53​ cm

6. Kết luận

Hệ thức lượng trong tam giác vuông là một phần không thể thiếu trong toán học và có nhiều ứng dụng thực tế. Việc hiểu và áp dụng đúng các hệ thức này sẽ giúp chúng ta giải quyết nhiều bài toán một cách hiệu quả và chính xác.

Hy vọng bài viết này sẽ giúp bạn hiểu rõ hơn về hệ thức lượng trong tam giác vuông. Nếu bạn cần thêm thông tin hoặc có câu hỏi nào khác, hãy cho tôi biết nhé!