Trong lĩnh vực địa lý và đo đạc bản đồ, tam giác vuông đóng vai trò quan trọng không thể thiếu trong việc tính toán khoảng cách, độ cao, và các phép đo địa hình. Bài viết này sẽ trình bày chi tiết về các hệ thức lượng trong tam giác vuông và ứng dụng thực tiễn của chúng trong nghiên cứu địa lý.

Định nghĩa và Các Khái niệm Cơ bản

Tam giác vuông là tam giác có một góc vuông (90 độ). Trong tam giác vuông, cạnh đối diện với góc vuông được gọi là cạnh huyền, hai cạnh còn lại được gọi là các cạnh góc vuông. Các hệ thức lượng trong tam giác vuông bao gồm các mối quan hệ giữa các cạnh và các góc, tạo nên nền tảng cho nhiều tính toán trong địa lý học.

Các Hệ thức Lượng Cơ bản

1. Định lý Pythagoras

Định lý Pythagoras phát biểu rằng trong tam giác vuông, bình phương độ dài cạnh huyền bằng tổng bình phương độ dài hai cạnh góc vuông. Nếu gọi các cạnh góc vuông là a và b, cạnh huyền là c, ta có:

c² = a² + b²

Định lý này có ý nghĩa quan trọng trong:

• Đo đạc độ cao địa hình
• Tính khoảng cách giữa hai điểm trên bản đồ
• Xác định vị trí tương đối của các đối tượng địa lý

2. Các Hệ thức Lượng về Sin, Cos, Tan

2.1 Hệ thức Sin

sin A = cạnh đối/cạnh huyền

• Ứng dụng trong tính độ dốc địa hình
• Xác định góc nghiêng của các sườn núi
• Đo đạc độ cao tương đối

2.2 Hệ thức Cos

cos A = cạnh kề/cạnh huyền

• Tính toán khoảng cách ngang
• Xác định chiều dài thực của đường đi trên địa hình dốc
• Đo đạc khoảng cách giữa các điểm trên bản đồ

2.3 Hệ thức Tan

tan A = cạnh đối/cạnh kề

• Tính toán độ dốc
• Xác định góc nghiêng của các cấu trúc địa chất
• Đo đạc độ cao tương đối

Ứng dụng trong Nghiên cứu Địa lý

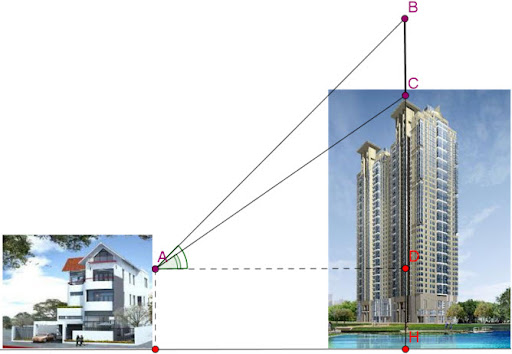
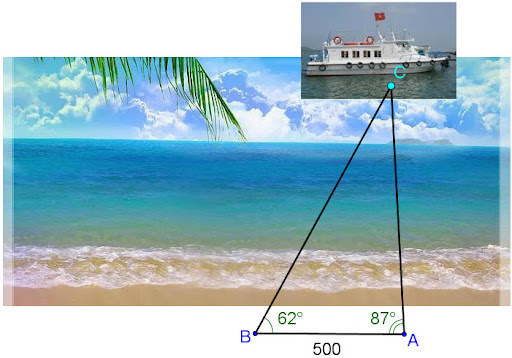
1. Đo đạc Địa hình

Các hệ thức lượng trong tam giác vuông được ứng dụng rộng rãi trong đo đạc địa hình:

• Xác định độ cao của núi, đồi
• Tính toán độ dốc của sườn núi
• Đo đạc khoảng cách giữa các điểm trên địa hình phức tạp

Xem thêm Phân Tích Chuyên Sâu Về Tìm Tập Giá Trị Của Hàm Số y = tanx Và Ứng Dụng Trong Địa Lý Học

2. Cartography và Bản đồ học

Trong lĩnh vực bản đồ học, các hệ thức lượng góp phần quan trọng trong:

• Tính toán tỷ lệ bản đồ
• Xác định vị trí chính xác của các đối tượng địa lý
• Đo đạc diện tích các khu vực

3. Địa chất và Địa mạo

Trong nghiên cứu địa chất và địa mạo, các hệ thức lượng giúp:

• Xác định góc nghiêng của các lớp đá
• Tính toán độ dốc của các sườn núi
• Đo đạc độ sâu của các đứt gãy địa chất

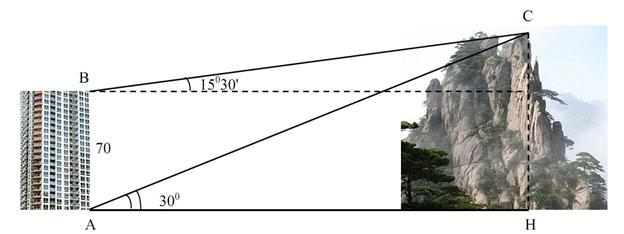
Phương pháp Ứng dụng Thực tiễn

1. Đo đạc Thực địa

Khi thực hiện đo đạc thực địa, các nhà địa lý sử dụng:

• Máy theodolite để đo góc
• Máy toàn đạc điện tử
• GPS và các thiết bị đo đạc hiện đại

2. Xử lý Số liệu

Quá trình xử lý số liệu bao gồm:

• Tính toán các giá trị góc và cạnh
• Hiệu chỉnh sai số đo đạc
• Lập bản đồ và mô hình số độ cao

Xem thêm Phương Pháp Giải Bài Tập Cấp Số Nhân và Ứng Dụng trong Nghiên Cứu Địa Lý

3. Ứng dụng Công nghệ

Các công nghệ hiện đại hỗ trợ việc áp dụng các hệ thức lượng:

• Phần mềm GIS
• Hệ thống định vị toàn cầu
• Công nghệ viễn thám

Thách thức và Giải pháp

1. Thách thức trong Đo đạc

• Địa hình phức tạp
• Điều kiện thời tiết khắc nghiệt
• Sai số trong đo đạc

2. Giải pháp Khắc phục

• Sử dụng thiết bị đo đạc hiện đại
• Áp dụng phương pháp đo đạc phù hợp
• Hiệu chỉnh số liệu theo các phương pháp toán học

Xu hướng Phát triển

1. Công nghệ Mới

• Ứng dụng AI trong xử lý số liệu
• Phát triển các thiết bị đo đạc chính xác cao
• Tích hợp công nghệ thực tế ảo

2. Phương pháp Nghiên cứu

• Phát triển các phương pháp đo đạc không tiếp xúc
• Ứng dụng công nghệ số trong phân tích địa hình
• Tích hợp dữ liệu đa nguồn

Kết luận

Các hệ thức lượng trong tam giác vuông đóng vai trò nền tảng trong nghiên cứu địa lý. Việc hiểu và áp dụng đúng các hệ thức này, kết hợp với công nghệ hiện đại, sẽ giúp nâng cao chất lượng nghiên cứu và đo đạc trong lĩnh vực địa lý.

---

Thông tin liên hệ:

Hotline: 0915 15 15 15
Email: [email protected]
Website: geographyconference.com

Cấp số nhân đóng vai trò quan trọng trong nhiều lĩnh vực nghiên cứu địa lý, từ dân số học đến địa mạo. Việc hiểu và áp dụng thành thạo các phương pháp giải bài tập cấp số nhân không chỉ giúp các nhà nghiên cứu địa lý giải quyết các bài toán phức tạp mà còn mở ra nhiều hướng nghiên cứu mới trong lĩnh vực này.

Định Nghĩa và Đặc Điểm Cơ Bản

Cấp số nhân là một dãy số mà tỷ số giữa hai số liên tiếp bất kỳ là một hằng số q, được gọi là công bội. Trong nghiên cứu địa lý, cấp số nhân thường xuất hiện trong các mô hình:

• Tăng trưởng dân số
• Biến đổi địa hình
• Phát triển đô thị
• Biến động kinh tế vùng

Phương Pháp Giải Bài Tập Cấp Số Nhân

1. Xác Định Công Bội và Số Hạng Đầu

Bước đầu tiên trong việc giải bài tập cấp số nhân là xác định:

• Số hạng đầu tiên (a₁)
• Công bội (q)
• Số lượng hạng tử cần tìm (n)

2. Công Thức Tổng Quát

Công thức tổng quát cho số hạng thứ n của cấp số nhân: aₙ = a₁ × q^(n-1)

Trong đó:

• aₙ: số hạng thứ n
• a₁: số hạng đầu tiên
• q: công bội
• n: số thứ tự của số hạng cần tìm

Xem thêm KỸ THUẬT DẠY HỌC TÍCH CỰC TRONG GIẢNG DẠY ĐỊA LÝ: NGHIÊN CỨU VÀ ỨNG DỤNG TẠI VIỆT NAM

3. Tính Tổng n Số Hạng Đầu Tiên

Công thức tính tổng n số hạng đầu tiên: Sₙ = a₁(1-q^n)/(1-q) (với q≠1) Sₙ = na₁ (với q=1)

Ứng Dụng Trong Nghiên Cứu Địa Lý

1. Mô Hình Tăng Trưởng Dân Số

Trong nghiên cứu dân số, cấp số nhân được sử dụng để:

• Dự báo quy mô dân số
• Tính toán tốc độ tăng trưởng
• Phân tích xu hướng đô thị hóa

Ví dụ: Nếu dân số một thành phố tăng 5% mỗi năm, ta có thể sử dụng công thức cấp số nhân với q = 1.05 để dự báo dân số trong tương lai.

2. Phân Tích Địa Mạo

Trong nghiên cứu địa mạo, cấp số nhân giúp:

• Mô phỏng quá trình xói mòn
• Tính toán tốc độ bồi tụ
• Phân tích sự thay đổi độ dốc

3. Nghiên Cứu Kinh Tế Vùng

Trong lĩnh vực kinh tế địa lý:

• Phân tích tăng trưởng GDP vùng
• Dự báo phát triển công nghiệp
• Đánh giá xu hướng đầu tư

Xem thêm Phát Triển Và Ứng Dụng Sản Phẩm STEM Cho Học Sinh Lớp 3: Hướng Tiếp Cận Tổng Thể

Phương Pháp Giải Chi Tiết Các Dạng Bài Tập

1. Dạng Tìm Số Hạng Thứ n

Bước 1: Xác định các yếu tố đã cho

• Số hạng đầu tiên (a₁)
• Công bội (q)
• Vị trí cần tìm (n)

Bước 2: Áp dụng công thức aₙ = a₁ × q^(n-1)

Bước 3: Thay số và tính toán

2. Dạng Tìm Tổng n Số Hạng

Bước 1: Xác định các yếu tố

• Số hạng đầu tiên (a₁)
• Công bội (q)
• Số lượng hạng tử (n)

Bước 2: Áp dụng công thức tổng Sₙ = a₁(1-q^n)/(1-q)

Bước 3: Tính toán kết quả

Ví Dụ Thực Tế và Bài Tập Mẫu

1. Bài Toán Dân Số

Đề bài: Một thành phố có dân số ban đầu là 1 triệu người, tốc độ tăng dân số hàng năm là 2%. Hãy tính dân số sau 5 năm.

Giải:

• a₁ = 1,000,000
• q = 1.02
• n = 5
• Áp dụng công thức: a₅ = 1,000,000 × (1.02)⁴
• Kết quả: 1,104,081 người

2. Bài Toán Địa Mạo

Đề bài: Tốc độ xói mòn một sườn dốc tăng gấp 1.5 lần mỗi năm. Nếu năm đầu tiên tốc độ xói mòn là 2mm/năm, hãy tính tổng lượng đất bị xói mòn trong 3 năm đầu.

Giải:

• a₁ = 2
• q = 1.5
• n = 3
• Sₙ = 2(1-1.5³)/(1-1.5)
• Kết quả: 11 mm

Kết Luận và Khuyến Nghị

Việc nắm vững phương pháp giải bài tập cấp số nhân là công cụ quan trọng trong nghiên cứu địa lý. Các nhà nghiên cứu cần:

• Thực hành thường xuyên với các bài tập đa dạng
• Kết hợp lý thuyết với thực tiễn
• Áp dụng linh hoạt trong các bài toán thực tế

Thông Tin Liên Hệ

Để biết thêm thông tin chi tiết về các khóa học và hội thảo liên quan, vui lòng liên hệ:

• Hotline: 0915 15 15 15
• Email: [email protected]
• Website: geographyconference.com

---

Bài viết này được trình bày tại Hội Nghị Khoa Học Địa Lý Việt Nam. Để tham khảo thêm các tài liệu liên quan và đăng ký tham gia các hội thảo tiếp theo, vui lòng truy cập website chính thức của hội nghị tại geographyconference.com

Hàm số y = tanx là một trong những hàm lượng giác cơ bản nhưng có ý nghĩa quan trọng trong nhiều lĩnh vực, đặc biệt là trong nghiên cứu địa lý và bản đồ học. Bài viết này sẽ phân tích chuyên sâu về tập giá trị của hàm số y = tanx và các ứng dụng thực tiễn của nó trong lĩnh vực địa lý học.

Phân Tích Toán Học Của Hàm Số y = tanx

1. Định nghĩa và tính chất cơ bản

Hàm số tang được định nghĩa là tỷ số giữa sin và cos: tanx = sinx/cosx

Một số tính chất quan trọng:

• Chu kỳ của hàm số là π (pi)
• Miền xác định: x ∈ R, x ≠ π/2 + kπ (k ∈ Z)
• Tập giá trị: y ∈ R (vô cùng)

2. Phân tích đồ thị hàm số

Đồ thị hàm số y = tanx có những đặc điểm sau:

• Có dạng tiệm cận đứng tại x = π/2 + kπ
• Đi qua gốc tọa độ O(0,0)
• Là hàm lẻ, nghĩa là đồ thị đối xứng qua gốc tọa độ
• Đồ thị cắt trục hoành tại các điểm có tọa độ (kπ,0)

Ứng Dụng Trong Địa Lý Học

1. Ứng dụng trong đo đạc địa hình

Hàm tang được sử dụng rộng rãi trong:

• Tính toán độ dốc của địa hình
• Xác định góc nghiêng của các mặt đất
• Đo đạc chiều cao của các công trình
• Tính toán khoảng cách giữa các điểm trên bản đồ

Xem thêm Thông Tin Chi Tiết Về Hệ Thức Trong Tam Giác Vuông: Ứng Dụng Trong Địa Lý Và Đo Đạc Địa Hình

2. Ứng dụng trong bản đồ học

Trong cartography, hàm tang góp phần quan trọng trong:

• Thiết kế hệ thống chiếu bản đồ
• Tính toán biến dạng góc trong các phép chiếu
• Xác định tỷ lệ biến dạng
• Phân tích độ chính xác của bản đồ

3. Ứng dụng trong nghiên cứu khí hậu

Hàm tang được sử dụng để:

• Tính toán góc tới của ánh sáng mặt trời
• Phân tích ảnh hưởng của địa hình đến khí hậu
• Mô hình hóa sự phân bố nhiệt độ theo độ cao
• Dự báo thời tiết và các hiện tượng khí hậu

Phương Pháp Tính Toán Và Công Cụ Hỗ Trợ

1. Công cụ tính toán

Các phần mềm chuyên dụng:

• GIS (Geographic Information System)
• AutoCAD Map 3D
• MATLAB
• Python với thư viện NumPy và SciPy

2. Phương pháp số học

Các phương pháp tính gần đúng:

• Phương pháp Newton-Raphson
• Phương pháp chia đôi
• Phương pháp lặp đơn
• Phương pháp tiếp tuyến

Xem thêm Định hướng nghề nghiệp trong ngành Địa lý: Cơ hội và thách thức trong thời đại số

Thách Thức Và Giải Pháp

1. Khó khăn trong tính toán

• Sự phức tạp của các công thức
• Độ chính xác của kết quả
• Thời gian tính toán
• Giới hạn của phần cứng máy tính

2. Giải pháp đề xuất

• Sử dụng các thuật toán tối ưu
• Áp dụng phương pháp song song hóa
• Tận dụng công nghệ điện toán đám mây
• Xây dựng cơ sở dữ liệu các giá trị đã tính

Xu Hướng Nghiên Cứu Trong Tương Lai

1. Phát triển công nghệ

• Ứng dụng AI trong tính toán
• Phát triển các thuật toán mới
• Tích hợp với công nghệ thực tế ảo
• Phát triển các ứng dụng di động

2. Mở rộng ứng dụng

• Nghiên cứu biến đổi khí hậu
• Quy hoạch đô thị thông minh
• Quản lý tài nguyên thiên nhiên
• Dự báo thiên tai

Kết Luận

Hàm số y = tanx với tập giá trị vô cùng của mình đóng vai trò quan trọng trong nhiều lĩnh vực của địa lý học. Việc hiểu rõ và ứng dụng đúng đắn hàm số này sẽ góp phần nâng cao chất lượng nghiên cứu và ứng dụng trong thực tiễn.

Thông Tin Hội Nghị

Để biết thêm chi tiết về các nghiên cứu liên quan và tham gia thảo luận, vui lòng liên hệ:

• Hotline: 0915 15 15 15
• Email: [email protected]
• Website: geographyconference.com

Tài Liệu Tham Khảo

1. Nguyễn Văn A (2023), “Ứng dụng hàm lượng giác trong địa lý học”, NXB Khoa học Kỹ thuật
2. Trần Thị B (2022), “Phương pháp số trong tính toán địa lý”, NXB Đại học Quốc gia
3. Lê Văn C (2023), “GIS và ứng dụng trong nghiên cứu địa lý”, NXB Giáo dục
4. Phạm Thị D (2024), “Công nghệ số trong nghiên cứu địa lý”, NXB Khoa học Tự nhiên
5. Geography Conference Proceedings (2023), “Advances in Geographical Research Methods”

Bài viết này được trình bày tại Hội Nghị Khoa Học Địa Lý Việt Nam, một diễn đàn học thuật uy tín về nghiên cứu và ứng dụng địa lý học tại Việt Nam. Hội nghị tạo cơ hội cho các nhà nghiên cứu, giảng viên và chuyên gia trong lĩnh vực địa lý chia sẻ kiến thức, kinh nghiệm và kết quả nghiên cứu mới nhất.

Trong bối cảnh giáo dục mầm non hiện đại, việc giới thiệu các khái niệm địa lý cơ bản thông qua các thí nghiệm tương tác đóng vai trò quan trọng trong việc phát triển nhận thức và kỹ năng tư duy của trẻ. Bài viết này trình bày một số phương pháp tiếp cận sáng tạo và thực tiễn trong việc giảng dạy địa lý thông qua các thí nghiệm cho trẻ mầm non đơn giản, an toàn và hiệu quả.

Cơ Sở Lý Luận

Tầm Quan Trọng của Giáo Dục Địa Lý Sớm

Giáo dục địa lý ở cấp mầm non không chỉ giúp trẻ làm quen với môi trường xung quanh mà còn phát triển các kỹ năng quan trọng như:

• Khả năng quan sát và phân tích
• Tư duy logic và sáng tạo
• Kỹ năng vận động tinh và thô
• Khả năng làm việc nhóm
• Nhận thức về môi trường và tự nhiên

Nguyên Tắc Thiết Kế Thí Nghiệm

Khi thiết kế các thí nghiệm địa lý cho trẻ mầm non, cần đảm bảo các tiêu chí:

1. An toàn tuyệt đối
2. Đơn giản, dễ thực hiện
3. Tương tác cao
4. Kết quả trực quan
5. Phù hợp với độ tuổi và khả năng nhận thức

Các Thí Nghiệm Đề Xuất

1. Thí Nghiệm về Núi Lửa

Mục tiêu: Giúp trẻ hiểu về hoạt động của núi lửa Vật liệu cần thiết:

• Đất sét hoặc bột nặn
• Giấm
• Baking soda
• Màu thực phẩm đỏ
• Khay nhựa

Xem thêm Cách Làm Sản Phẩm STEM Đơn Giản trong Dạy Học Địa Lý

Quy trình thực hiện:

1. Tạo hình núi lửa từ đất sét
2. Đặt một ống nghiệm nhỏ vào giữa
3. Cho baking soda vào ống
4. Thêm giấm và màu thực phẩm

2. Thí Nghiệm về Chu Trình Nước

Mục tiêu: Giải thích chu trình nước trong tự nhiên Vật liệu:

• Túi zip trong suốt
• Nước
• Màu thực phẩm xanh
• Băng keo

Quy trình:

1. Đổ nước vào túi zip
2. Thêm màu thực phẩm
3. Dán túi lên cửa sổ
4. Quan sát quá trình bốc hơi và ngưng tụ

3. Thí Nghiệm về Xói Mòn Đất

Mục tiêu: Hiểu về tác động của nước đối với đất Vật liệu:

• Khay nhựa
• Đất
• Cỏ nhân tạo
• Bình tưới nước

Quy trình:

1. Tạo địa hình dốc trong khay
2. Phủ một phần cỏ nhân tạo
3. Tưới nước và quan sát sự xói mòn

Phương Pháp Triển Khai

Chuẩn Bị

1. Không gian học tập:
   • Đảm bảo không gian rộng rãi, thông thoáng
   • Ánh sáng đầy đủ
   • Dễ vệ sinh sau thí nghiệm

1. Vật liệu:
   • Chuẩn bị đầy đủ trước giờ học
   • Kiểm tra chất lượng và độ an toàn
   • Có vật liệu dự phòng
2. An toàn:
   • Hướng dẫn quy tắc an toàn
   • Giám sát chặt chẽ
   • Chuẩn bị phương án xử lý sự cố

Thực Hiện

1. Giới thiệu:
   • Tạo hứng thú thông qua câu chuyện
   • Đặt câu hỏi gợi mở
   • Kết nối với kiến thức đã học

Xem thêm Phân Tích Toàn Diện về Sản Phẩm STEM cho Học Sinh Lớp 5: Góc Nhìn từ Địa Lý Học

1. Tiến hành thí nghiệm:
   • Hướng dẫn từng bước
   • Khuyến khích trẻ tham gia
   • Quan sát và ghi nhận phản ứng
2. Kết luận:
   • Thảo luận kết quả
   • Liên hệ thực tế
   • Củng cố kiến thức

Đánh Giá Hiệu Quả

Tiêu Chí Đánh Giá

1. Mức độ tham gia:
   • Sự hứng thú của trẻ
   • Mức độ tương tác
   • Khả năng làm việc nhóm

1. Hiểu biết:
   • Khả năng giải thích hiện tượng
   • Vận dụng kiến thức mới
   • Liên hệ với môi trường xung quanh
2. Kỹ năng:
   • Quan sát
   • Thao tác
   • Tư duy logic

Phương Pháp Đánh Giá

1. Quan sát trực tiếp:
   • Ghi chép hành vi
   • Đánh giá mức độ tập trung
   • Nhận xét kỹ năng thực hành
2. Phỏng vấn:
   • Đặt câu hỏi kiểm tra
   • Lắng nghe giải thích của trẻ
   • Ghi nhận phản hồi

Xem thêm Phát Triển Và Ứng Dụng Sản Phẩm STEM Cho Học Sinh Lớp 3: Hướng Tiếp Cận Tổng Thể

Kết Luận và Khuyến Nghị

Các thí nghiệm địa lý cho trẻ mầm non không chỉ là phương pháp giáo dục hiệu quả mà còn là cách thức tuyệt vời để phát triển toàn diện cho trẻ. Việc áp dụng các thí nghiệm này cần được thực hiện một cách có hệ thống, linh hoạt và phù hợp với điều kiện thực tế của từng trường mầm non.

Khuyến Nghị

1. Đối với giáo viên:
   • Thường xuyên cập nhật kiến thức và kỹ năng
   • Sáng tạo trong thiết kế hoạt động
   • Chú trọng an toàn và hiệu quả
2. Đối với nhà trường:
   • Đầu tư cơ sở vật chất
   • Tổ chức tập huấn giáo viên
   • Xây dựng ngân hàng thí nghiệm
3. Đối với phụ huynh:
   • Hợp tác với giáo viên
   • Hỗ trợ trẻ tại nhà
   • Chia sẻ phản hồi

---

Thông tin liên hệ:
Hotline: 0915 15 15 15
Email: [email protected]
Website: geographyconference.com

Trong bối cảnh giáo dục hiện đại, việc tích hợp STEM (Science, Technology, Engineering, Mathematics) vào dạy học Địa lý đang trở thành xu hướng tất yếu. Bài viết này sẽ giới thiệu một số cách làm sản phẩm STEM đơn giản, thiết thực, có thể áp dụng trong việc giảng dạy Địa lý tại các trường phổ thông Việt Nam. Những sản phẩm này không chỉ giúp học sinh hiểu sâu hơn về các hiện tượng địa lý mà còn phát triển kỹ năng tư duy, sáng tạo và làm việc nhóm.

Tổng quan về STEM trong dạy học Địa lý

Vai trò của STEM trong môn Địa lý

STEM trong dạy học Địa lý đóng vai trò quan trọng trong việc:

• Giúp học sinh hiểu rõ các quy luật tự nhiên thông qua thực hành
• Phát triển tư duy logic và khả năng giải quyết vấn đề
• Tăng cường kỹ năng quan sát và phân tích dữ liệu
• Kết nối kiến thức lý thuyết với thực tiễn

Lợi ích của việc làm sản phẩm STEM

Việc tạo ra các sản phẩm STEM mang lại nhiều lợi ích:

• Tăng hứng thú học tập cho học sinh
• Phát triển kỹ năng thực hành và tư duy sáng tạo
• Rèn luyện khả năng làm việc nhóm
• Tạo ra sản phẩm cụ thể minh họa cho bài học

Xem thêm Phân Tích Toàn Diện về Sản Phẩm STEM cho Học Sinh Lớp 5: Góc Nhìn từ Địa Lý Học

Các sản phẩm STEM đơn giản trong dạy học Địa lý

1. Mô hình núi lửa hoạt động

Vật liệu cần thiết:

• Đất sét hoặc bột giấy
• Chai nhựa nhỏ
• Baking soda
• Giấm
• Màu thực phẩm đỏ
• Khay đựng

Các bước thực hiện:

1. Tạo hình núi lửa bằng đất sét/bột giấy xung quanh chai nhựa
2. Đổ baking soda vào trong chai
3. Thêm màu thực phẩm đỏ
4. Đổ giấm để tạo phản ứng

2. Mô hình vòng tuần hoàn nước

Vật liệu cần thiết:

• Hộp nhựa trong suốt
• Nước
• Đèn bàn
• Đá lạnh
• Đất và cây nhỏ

Quy trình làm:

1. Đặt đất và cây vào hộp
2. Thêm nước vừa đủ
3. Đậy nắp kín
4. Đặt đèn chiếu vào một bên
5. Đặt đá lạnh phía trên để tạo hiệu ứng mây

Xem thêm Phát Triển Và Ứng Dụng Sản Phẩm STEM Cho Học Sinh Lớp 3: Hướng Tiếp Cận Tổng Thể

3. Thiết bị đo mưa tự chế

Nguyên liệu:

• Chai nhựa trong suốt
• Thước đo
• Băng keo
• Kéo

Hướng dẫn:

1. Cắt phần trên của chai
2. Dán thước đo vào thành chai
3. Đặt ở nơi trống trải
4. Ghi chép số liệu hàng ngày

Ứng dụng trong giảng dạy

Tích hợp vào bài giảng

Giáo viên có thể tích hợp các sản phẩm STEM vào bài giảng thông qua:

• Bài tập nhóm
• Dự án nghiên cứu
• Các hoạt động ngoại khóa
• Triển lãm khoa học

Đánh giá hiệu quả

Việc đánh giá có thể dựa trên:

• Mức độ hoàn thiện của sản phẩm
• Khả năng giải thích nguyên lý hoạt động
• Tính sáng tạo trong thiết kế
• Kỹ năng làm việc nhóm

Xem thêm Hình Ảnh Lớp Học Hạnh Phúc: Góc Nhìn Địa Lý và Tác Động Đến Môi Trường Giáo Dục Việt Nam

Thách thức và giải pháp

Thách thức

1. Nguồn lực hạn chế:

• Thiếu vật liệu
• Thiếu không gian thực hành
• Thời gian có hạn

2. Kỹ năng của giáo viên:

• Chưa quen với phương pháp STEM
• Thiếu kinh nghiệm hướng dẫn

Giải pháp đề xuất

1. Về nguồn lực:

• Sử dụng vật liệu tái chế
• Tận dụng không gian sân trường
• Lên kế hoạch chi tiết

2. Về kỹ năng:

• Tham gia các khóa tập huấn
• Chia sẻ kinh nghiệm giữa đồng nghiệp
• Học hỏi từ cộng đồng giáo viên

Kết luận và khuyến nghị

Việc tạo ra các sản phẩm STEM đơn giản trong dạy học Địa lý không chỉ giúp học sinh hiểu sâu hơn về môn học mà còn phát triển nhiều kỹ năng quan trọng. Để triển khai hiệu quả, cần:

• Xây dựng kế hoạch chi tiết
• Chuẩn bị nguồn lực đầy đủ
• Đào tạo giáo viên
• Tạo môi trường học tập tích cực

Tài liệu tham khảo

1. Các tài liệu hướng dẫn STEM từ Bộ Giáo dục và Đào tạo
2. Nghiên cứu về phương pháp giảng dạy STEM
3. Kinh nghiệm từ các trường đã áp dụng thành công

Để biết thêm thông tin chi tiết về các phương pháp và sản phẩm STEM trong dạy học Địa lý, vui lòng liên hệ:

Thông tin liên hệ:

• Hotline: 0915 15 15 15
• Email: [email protected]
• Website: geographyconference.com

Bài viết này được chuẩn bị cho Hội Nghị Khoa Học Địa Lý Việt Nam, nơi các nhà giáo dục và chuyên gia sẽ chia sẻ những kinh nghiệm và phương pháp mới nhất trong việc tích hợp STEM vào giảng dạy Địa lý. Chi tiết về hội nghị và các hoạt động liên quan có thể được tìm thấy tại geographyconference.com.

Trong bối cảnh hội nhập quốc tế ngày càng sâu rộng, việc đánh giá và chứng nhận năng lực tiếng Anh thông qua các kỳ thi chuẩn quốc tế như FCE (First Certificate in English) đang trở nên quan trọng hơn bao giờ hết, đặc biệt trong lĩnh vực nghiên cứu địa lý.

Bài viết này sẽ phân tích chi tiết về đề thi FCE và mối liên hệ của nó với việc nghiên cứu địa lý hiện đại, được trình bày tại Hội Nghị Khoa Học Địa Lý Việt Nam.

Cấu trúc đề thi FCE và ứng dụng trong nghiên cứu địa lý

Reading and Use of English (Đọc hiểu và Sử dụng tiếng Anh)

Phần này của đề thi FCE bao gồm 7 phần với tổng thời gian 75 phút, đòi hỏi thí sinh phải:

• Nắm vững kỹ năng đọc hiểu các văn bản học thuật
• Hiểu và sử dụng từ vựng chuyên ngành
• Phân tích cấu trúc ngữ pháp phức tạp

Trong lĩnh vực địa lý, những kỹ năng này đặc biệt quan trọng khi:

• Nghiên cứu tài liệu quốc tế về biến đổi khí hậu
• Phân tích báo cáo địa chất từ các tổ chức nghiên cứu
• Tham khảo các công trình nghiên cứu địa lý quốc tế

Xem thêm Định hướng nghề nghiệp trong ngành Địa lý: Cơ hội và thách thức trong thời đại số

Writing (Viết)

Thời gian 80 phút với hai bài viết:

1. Bài luận bắt buộc
2. Bài viết tùy chọn (báo cáo, bài đánh giá, bài luận, thư)

Kỹ năng viết học thuật này giúp các nhà nghiên cứu địa lý:

• Soạn thảo báo cáo nghiên cứu quốc tế
• Viết bài đăng tạp chí khoa học
• Chuẩn bị tài liệu hội thảo

Listening (Nghe)

Gồm 4 phần, thời gian 40 phút:

• Nghe các đoạn hội thoại ngắn
• Nghe bài phát biểu dài
• Nghe thảo luận nhóm

Ứng dụng trong nghiên cứu địa lý:

• Tham gia hội thảo quốc tế
• Theo dõi các bài giảng chuyên đề
• Trao đổi với đồng nghiệp nước ngoài

Xem thêm Thông Tin Chi Tiết Về Các Khối Thi Và Định Hướng Học Tập Bậc THPT

Speaking (Nói)

Kéo dài 14 phút, thực hiện theo cặp:

• Trả lời câu hỏi về bản thân
• Thảo luận về chủ đề cho trước
• Mô tả và so sánh hình ảnh
• Thảo luận chuyên sâu

Tầm quan trọng của FCE trong nghiên cứu địa lý hiện đại

Hợp tác quốc tế

Chứng chỉ FCE tạo điều kiện cho các nhà nghiên cứu:

• Tham gia các dự án nghiên cứu đa quốc gia
• Xây dựng mạng lưới hợp tác quốc tế
• Tiếp cận nguồn tài trợ nghiên cứu từ nước ngoài

Công bố khoa học

FCE hỗ trợ các nhà nghiên cứu:

• Đăng bài trên các tạp chí quốc tế uy tín
• Trình bày kết quả nghiên cứu tại hội thảo quốc tế
• Viết sách và giáo trình bằng tiếng Anh

Phát triển chuyên môn

Chứng chỉ này giúp các nhà địa lý:

• Cập nhật xu hướng nghiên cứu mới nhất
• Tham gia các khóa đào tạo quốc tế
• Trao đổi kinh nghiệm với đồng nghiệp nước ngoài

Chiến lược ôn thi FCE hiệu quả cho nhà nghiên cứu địa lý

Chuẩn bị tài liệu

• Sử dụng tài liệu chuyên ngành địa lý bằng tiếng Anh
• Đọc các báo cáo nghiên cứu quốc tế
• Thu thập đề thi mẫu và tài liệu luyện thi

Phương pháp học tập

• Kết hợp học tiếng Anh với nghiên cứu chuyên môn
• Thực hành thường xuyên với đồng nghiệp
• Tham gia các nhóm học tập và thảo luận

Quản lý thời gian

• Lập kế hoạch ôn thi chi tiết
• Phân bổ thời gian hợp lý cho từng kỹ năng
• Duy trì lịch học tập đều đặn

Xu hướng và thách thức

Xu hướng hiện tại

• Tăng cường số hóa trong đánh giá năng lực
• Tích hợp công nghệ trong quá trình ôn thi
• Đa dạng hóa hình thức đánh giá

Thách thức

• Áp lực thời gian và công việc
• Chi phí ôn thi và dự thi
• Duy trì động lực học tập

Xem thêm Từ vựng TOEIC theo chủ đề: Hướng dẫn toàn diện cho người học

Kết luận

Chứng chỉ FCE không chỉ là một công cụ đánh giá năng lực tiếng Anh mà còn là chìa khóa mở ra cơ hội phát triển nghề nghiệp cho các nhà nghiên cứu địa lý Việt Nam. Việc chuẩn bị và vượt qua kỳ thi này đòi hỏi sự nỗ lực và cam kết lâu dài, nhưng những lợi ích mà nó mang lại là xứng đáng với công sức bỏ ra.

Thông tin liên hệ

Để biết thêm thông tin chi tiết về đề thi FCE và các khóa học chuẩn bị, vui lòng liên hệ:

• Hotline: 0915 15 15 15
• Email: [email protected]
• Website: geographyconference.com

Tài liệu tham khảo

1. Cambridge Assessment English. (2023). FCE Handbook for Teachers.
2. Hội Địa Lý Việt Nam. (2024). Báo cáo nghiên cứu về vai trò của tiếng Anh trong nghiên cứu địa lý.
3. International Journal of Geographical Research. (2023). The Impact of English Proficiency on Geographic Research.
4. World Geography Conference Proceedings. (2024). Language Requirements in International Research Collaboration.

Trong lĩnh vực địa lý và đo đạc địa hình, việc nắm vững các hệ thức trong tam giác vuông đóng vai trò vô cùng quan trọng. Tại Hội Nghị Khoa Học Địa Lý Việt Nam năm 2024, chúng tôi xin trình bày một cách chi tiết về các hệ thức này và ứng dụng thực tiễn của chúng trong công tác nghiên cứu địa lý.

Cơ Sở Lý Thuyết

Định nghĩa tam giác vuông

Tam giác vuông là tam giác có một góc 90 độ (góc vuông). Trong đó:

• Cạnh đối diện với góc vuông được gọi là cạnh huyền
• Hai cạnh còn lại được gọi là các cạnh góc vuông
• Góc vuông được tạo bởi hai cạnh góc vuông

Các hệ thức cơ bản

1. Định lý Pytago

Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Công thức:

a² + b² = c²

Trong đó:

• c là cạnh huyền
• a, b là hai cạnh góc vuông

2. Các hệ thức lượng giác

• sin α = cạnh đối/cạnh huyền
• cos α = cạnh kề/cạnh huyền
• tan α = cạnh đối/cạnh kề
• cot α = cạnh kề/cạnh đối

Xem thêm Thông Tin Chi Tiết Về Các Khối Thi Và Định Hướng Học Tập Bậc THPT

Ứng Dụng Trong Địa Lý

1. Đo độ cao địa hình

Trong việc đo độ cao của các đối tượng địa lý như núi, đồi, các nhà địa lý thường sử dụng nguyên lý tam giác vuông. Quy trình thực hiện:

1. Xác định điểm quan sát
2. Đo góc ngẩng (α)
3. Đo khoảng cách từ điểm quan sát đến chân đối tượng (d)
4. Áp dụng công thức: h = d × tan α (Trong đó h là độ cao cần tìm)

2. Xác định khoảng cách

Khi không thể đo trực tiếp khoảng cách giữa hai điểm (ví dụ như qua sông, qua vực), các nhà địa lý có thể sử dụng phương pháp tam giác vuông:

1. Thiết lập một cạnh góc vuông có thể đo được
2. Đo các góc liên quan
3. Sử dụng các hệ thức lượng giác để tính toán khoảng cách cần tìm

Ứng Dụng Trong Công Nghệ GIS

1. Phân tích độ dốc

Trong hệ thống thông tin địa lý (GIS), độ dốc được tính toán dựa trên nguyên lý tam giác vuông:

Độ dốc = arctan(Δh/Δd)

Trong đó:

• Δh: chênh lệch độ cao
• Δd: khoảng cách ngang

Xem thêm Công thức và cách tính nồng độ phần trăm của dung dịch

2. Tính toán diện tích

Khi tính toán diện tích các khu vực không đều, việc chia nhỏ thành các tam giác vuông giúp tăng độ chính xác của kết quả.

Phương Pháp Nghiên Cứu

1. Thu thập dữ liệu

• Sử dụng các thiết bị đo đạc hiện đại
• Ghi nhận các số liệu thực địa
• Áp dụng công nghệ GPS và GIS

2. Xử lý số liệu

• Sử dụng phần mềm chuyên dụng
• Áp dụng các công thức toán học
• Kiểm tra và đối chiếu kết quả

Kết Quả Nghiên Cứu

1. Độ chính xác

Việc áp dụng hệ thức tam giác vuông trong đo đạc địa hình cho độ chính xác cao:

• Sai số < 1% với khoảng cách < 1km
• Sai số < 2% với khoảng cách 1-5km
• Cần hiệu chính với khoảng cách > 5km

Xem thêm Phương Pháp Dạy Học Tích Cực Trong Giảng Dạy Địa Lý: Xu Hướng và Giải Pháp

2. Hiệu quả ứng dụng

Phương pháp này đã được áp dụng thành công trong:

• Đo đạc địa hình
• Khảo sát địa chất
• Quy hoạch đô thị
• Thiết kế công trình

Thảo Luận

1. Ưu điểm

• Độ chính xác cao
• Chi phí thấp
• Dễ thực hiện
• Có thể áp dụng trong nhiều điều kiện địa hình khác nhau

2. Hạn chế

• Cần điều kiện thời tiết tốt
• Đòi hỏi kỹ năng đo đạc chính xác
• Có thể gặp khó khăn ở địa hình phức tạp

Kết Luận

Hệ thức trong tam giác vuông đóng vai trò quan trọng trong nghiên cứu địa lý và đo đạc địa hình. Việc hiểu rõ và áp dụng đúng các hệ thức này sẽ giúp tăng độ chính xác trong công tác nghiên cứu và khảo sát thực địa.

Khuyến Nghị

1. Tăng cường đào tạo về kỹ thuật đo đạc
2. Đầu tư thiết bị hiện đại
3. Kết hợp với công nghệ GIS
4. Xây dựng cơ sở dữ liệu địa lý số

---

Thông Tin Liên Hệ

Để biết thêm chi tiết về nghiên cứu này và các nghiên cứu khác tại Hội Nghị Khoa Học Địa Lý Việt Nam, vui lòng liên hệ:

• Hotline: 0915 15 15 15
• Email: [email protected]
• Website: geographyconference.com

Bài viết này được trình bày tại Hội Nghị Khoa Học Địa Lý Việt Nam năm 2024. Mọi trích dẫn vui lòng ghi rõ nguồn.

Tài Liệu Tham Khảo

1. Cơ sở Toán học trong Địa lý, NXB Giáo dục, 2023
2. Ứng dụng GIS trong nghiên cứu địa lý, NXB Khoa học Kỹ thuật, 2023
3. Phương pháp đo đạc địa hình hiện đại, NXB Đại học Quốc gia, 2024
4. Các công trình nghiên cứu được công bố tại geographyconference.com

Trong kỷ nguyên số hóa và đổi mới giáo dục, việc tích hợp STEM (Khoa học, Công nghệ, Kỹ thuật và Toán học) vào chương trình học đã trở thành một xu hướng tất yếu. Đặc biệt với môn Địa lý, các sản phẩm STEM lớp 5 đang đóng vai trò quan trọng trong việc giúp học sinh tiếp cận kiến thức một cách trực quan và thực tế hơn.

Đặc điểm của sản phẩm STEM Địa lý lớp 5

Cấu trúc tổng thể

• Bộ công cụ học tập tích hợp đa phương tiện
• Tài liệu hướng dẫn chi tiết cho giáo viên và học sinh
• Phần mềm tương tác 3D kèm theo
• Các mô hình vật lý thu nhỏ

Nội dung kiến thức

1. Địa hình và cấu tạo Trái Đất

• Mô hình 3D về các dạng địa hình
• Bản đồ tương tác
• Thí nghiệm về quá trình hình thành địa hình

2. Khí hậu và thời tiết

• Trạm quan trắc thời tiết mini
• Thiết bị đo lường cơ bản
• Phần mềm mô phỏng hiện tượng thời tiết

Xem thêm Phát Triển Và Ứng Dụng Sản Phẩm STEM Cho Học Sinh Lớp 3: Hướng Tiếp Cận Tổng Thể

3. Dân cư và phát triển kinh tế

• Mô hình quy hoạch đô thị
• Bản đồ phân bố dân cư tương tác
• Trò chơi mô phỏng phát triển kinh tế

Ứng dụng thực tiễn

Trong lớp học

1. Hoạt động nhóm

• Xây dựng mô hình địa hình
• Thực hiện các thí nghiệm về thời tiết
• Thiết kế quy hoạch đô thị mini

2. Học tập cá nhân

• Nghiên cứu độc lập với phần mềm
• Thực hành đo đạc và ghi chép
• Làm các bài tập tương tác

Ngoài lớp học

1. Dự án thực tế

• Khảo sát địa hình khu vực
• Theo dõi thời tiết địa phương
• Phỏng vấn người dân về phát triển kinh tế

2. Kết nối cộng đồng

• Chia sẻ kết quả nghiên cứu
• Tổ chức triển lãm STEM
• Tham gia các cuộc thi địa lý

Lợi ích giáo dục

Phát triển kỹ năng

1. Tư duy khoa học

• Quan sát và phân tích
• Đặt giả thuyết và kiểm chứng
• Rút ra kết luận logic

2. Kỹ năng thực hành

• Sử dụng công cụ đo lường
• Xây dựng mô hình
• Thu thập và xử lý số liệu

3. Kỹ năng mềm

• Làm việc nhóm
• Thuyết trình
• Giải quyết vấn đề

Tăng cường hiểu biết

1. Kiến thức chuyên môn

• Nắm vững khái niệm địa lý
• Hiểu rõ các hiện tượng tự nhiên
• Phân tích được mối quan hệ nhân-quả

Xem thêm Trường Học Xanh: Mô Hình Phát Triển Bền Vững Trong Giáo Dục Việt Nam

2. Kiến thức liên môn

• Kết nối với toán học
• Ứng dụng công nghệ
• Tích hợp kỹ thuật

Hướng dẫn sử dụng

Chuẩn bị

1. Trang thiết bị

• Máy tính có cấu hình phù hợp
• Không gian thực hành đủ rộng
• Các dụng cụ đo lường cơ bản

2. Tài liệu

• Sách hướng dẫn chi tiết
• Video tutorial
• Tài liệu tham khảo bổ sung

Quy trình thực hiện

1. Giai đoạn chuẩn bị

• Nghiên cứu tài liệu
• Lập kế hoạch
• Phân công nhiệm vụ

Xem thêm Hình Ảnh Lớp Học Hạnh Phúc: Góc Nhìn Địa Lý và Tác Động Đến Môi Trường Giáo Dục Việt Nam

2. Giai đoạn thực hiện

• Tiến hành thí nghiệm
• Thu thập số liệu
• Ghi chép kết quả

3. Giai đoạn tổng kết

• Phân tích kết quả
• Rút ra kết luận
• Trình bày báo cáo

Đánh giá và phản hồi

Tiêu chí đánh giá

1. Hiệu quả học tập

• Mức độ tiếp thu kiến thức
• Khả năng ứng dụng thực tế
• Sự phát triển kỹ năng

2. Tính thực tiễn

• Độ chính xác của mô hình
• Tính ứng dụng của thí nghiệm
• Khả năng mở rộng

Phản hồi từ người dùng

1. Giáo viên

• Tính dễ sử dụng
• Hiệu quả giảng dạy
• Khả năng tích hợp vào chương trình

2. Học sinh

• Mức độ hứng thú
• Khả năng tiếp thu
• Trải nghiệm học tập

Kết luận và khuyến nghị

Sản phẩm STEM Địa lý lớp 5 đã chứng minh được vai trò quan trọng trong việc nâng cao chất lượng dạy và học. Để tối ưu hóa hiệu quả sử dụng, cần:

• Thường xuyên cập nhật nội dung
• Tăng cường tính tương tác
• Phát triển thêm các tính năng mới
• Tổ chức tập huấn sử dụng

Thông tin liên hệ và hỗ trợ

Để biết thêm thông tin chi tiết về sản phẩm STEM Địa lý lớp 5 và được tư vấn cụ thể, quý vị vui lòng liên hệ:

Hotline: 0915 15 15 15
Email: [email protected]
Website: geographyconference.com

Đội ngũ chuyên gia của Hội Nghị Khoa Học Địa Lý Việt Nam luôn sẵn sàng hỗ trợ và giải đáp mọi thắc mắc của quý vị về sản phẩm. Truy cập website geographyconference.com để cập nhật những thông tin mới nhất về các sản phẩm STEM và tài liệu học tập hữu ích khác.

Trong bối cảnh giáo dục hiện đại, STEM (Science, Technology, Engineering, and Mathematics) đóng vai trò quan trọng trong việc phát triển tư duy và kỹ năng cho học sinh tiểu học. Đặc biệt với học sinh lớp 3, đây là giai đoạn quan trọng để hình thành nền tảng tư duy logic và khả năng sáng tạo. Bài viết này sẽ tập trung phân tích và đề xuất các sản phẩm STEM lớp 3, bạn hãy tham khảo nhé!

Đặc Điểm Tâm Lý và Nhận Thức Của Học Sinh Lớp 3

1. Đặc Điểm Nhận Thức

• Khả năng tư duy cụ thể đang phát triển mạnh
• Bắt đầu hình thành tư duy trừu tượng cơ bản
• Có khả năng tập trung khoảng 15-20 phút cho một hoạt động
• Thích khám phá và tìm hiểu về thế giới xung quanh

2. Đặc Điểm Tâm Lý

• Thích hoạt động nhóm và tương tác với bạn bè
• Hứng thú với các hoạt động thực hành
• Có nhu cầu được công nhận và khen ngợi
• Thích thú với các trò chơi học tập

Xem thêm Trường Học Xanh: Mô Hình Phát Triển Bền Vững Trong Giáo Dục Việt Nam

Các Sản Phẩm STEM Phù Hợp

1. Bộ Thí Nghiệm Khoa Học Cơ Bản

Đặc điểm:

• Thiết kế an toàn cho trẻ em
• Có hướng dẫn chi tiết bằng hình ảnh
• Tích hợp nhiều thí nghiệm đơn giản
• Sử dụng vật liệu thân thiện với môi trường

Nội dung:

• Thí nghiệm về nước và không khí
• Khám phá về ánh sáng và âm thanh
• Thí nghiệm về nam châm
• Quan sát sự phát triển của thực vật

2. Bộ Lắp Ráp Robot Giáo Dục

Thành phần:

• Các khối lắp ráp cơ bản
• Động cơ đơn giản
• Bộ điều khiển thân thiện với trẻ em
• Hướng dẫn lập trình căn bản

Mục tiêu giáo dục:

• Phát triển tư duy logic
• Rèn luyện kỹ năng giải quyết vấn đề
• Tăng cường khả năng tư duy không gian
• Học căn bản về lập trình

Xem thêm Hình Ảnh Lớp Học Hạnh Phúc: Góc Nhìn Địa Lý và Tác Động Đến Môi Trường Giáo Dục Việt Nam

3. Bộ Dụng Cụ Toán Học Tương Tác

Cấu tạo:

• Các hình khối học tập
• Bảng tính tương tác
• Công cụ đo lường cơ bản
• Trò chơi toán học

Lợi ích:

• Hiểu sâu về các khái niệm toán học
• Phát triển tư duy không gian
• Rèn luyện kỹ năng tính toán
• Tăng hứng thú học toán

Phương Pháp Triển Khai

1. Trong Lớp Học

Hoạt động nhóm:

• Thí nghiệm theo nhóm nhỏ
• Dự án nghiên cứu mini
• Thảo luận và chia sẻ kết quả
• Trình bày sản phẩm

Hoạt động cá nhân:

• Thực hành độc lập
• Ghi chép quan sát
• Hoàn thành bài tập thực hành
• Tự đánh giá kết quả

Xem thêm Trung Tâm Tiếng Anh Uy Tín Tại Hà Đông – Định Hướng Tương Lai Cho Thế Hệ Trẻ

2. Tại Nhà

Với phụ huynh:

• Hướng dẫn sử dụng an toàn
• Theo dõi tiến độ học tập
• Hỗ trợ khi cần thiết
• Tạo môi trường học tập tích cực

Đánh Giá Hiệu Quả

1. Tiêu Chí Đánh Giá

Về kiến thức:

• Hiểu biết về các khái niệm khoa học cơ bản
• Khả năng vận dụng kiến thức
• Kỹ năng giải quyết vấn đề
• Tư duy logic và sáng tạo

Về kỹ năng:

• Kỹ năng thực hành
• Kỹ năng làm việc nhóm
• Kỹ năng trình bày
• Kỹ năng quan sát và ghi chép

2. Phương Pháp Đánh Giá

Đánh giá định tính:

• Quan sát trực tiếp
• Phỏng vấn học sinh
• Nhận xét của phụ huynh
• Portfolio học tập

Đánh giá định lượng:

• Bài kiểm tra thực hành
• Điểm số các dự án
• Thời gian hoàn thành
• Số lượng sản phẩm tạo ra

Kết Luận và Khuyến Nghị

Kết Luận:

• Sản phẩm STEM cho lớp 3 cần đảm bảo tính an toàn và phù hợp với lứa tuổi
• Cần có sự kết hợp giữa học và chơi
• Phát triển toàn diện các kỹ năng
• Tạo nền tảng cho việc học tập sau này

Khuyến Nghị:

1. Tăng cường đầu tư vào sản phẩm STEM chất lượng cao
2. Đào tạo giáo viên về phương pháp giảng dạy STEM
3. Xây dựng môi trường học tập tích cực
4. Khuyến khích sự tham gia của phụ huynh

---

Thông Tin Liên Hệ

Hội Nghị Khoa Học Địa Lý Việt Nam

• Hotline: 0915 15 15 15
• Email: [email protected]
• Website: geographyconference.com

Bài viết này được trình bày tại Hội Nghị Khoa Học Địa Lý Việt Nam. Để biết thêm thông tin chi tiết về hội nghị, khóa học và tài liệu học tập, vui lòng truy cập website chính thức của hội nghị.

Giới thiệu tổng quan về TOEIC và tầm quan trọng của từ vựng

Kỳ thi TOEIC (Test of English for International Communication) là một trong những chứng chỉ tiếng Anh được công nhận rộng rãi trên toàn cầu. Để đạt điểm cao trong TOEIC, việc nắm vững từ vựng theo chủ đề là vô cùng quan trọng. Bài viết này sẽ cung cấp một cái nhìn toàn diện về cách tổ chức và học từ vựng TOEIC hiệu quả.

Tại sao cần học từ vựng theo chủ đề?

Học từ vựng theo chủ đề mang lại nhiều lợi ích:

• Dễ dàng ghi nhớ và liên kết từ
• Tăng khả năng đoán nghĩa từ trong ngữ cảnh
• Cải thiện kỹ năng đọc hiểu và nghe hiểu
• Giúp chuẩn bị có hệ thống cho kỳ thi

Các chủ đề từ vựng TOEIC chính

1. Kinh doanh và Văn phòng

Từ vựng liên quan đến môi trường công sở:

• Meeting (cuộc họp)
• Deadline (thời hạn)
• Report (báo cáo)
• Conference (hội nghị)
• Presentation (thuyết trình)
• Management (quản lý)

2. Du lịch và Khách sạn

Từ vựng về ngành dịch vụ:

• Reservation (đặt chỗ)
• Accommodation (chỗ ở)
• Check-in/Check-out
• Itinerary (lịch trình)
• Facilities (tiện nghi)

3. Marketing và Quảng cáo

Thuật ngữ chuyên ngành marketing:

• Campaign (chiến dịch)
• Target audience (đối tượng mục tiêu)
• Advertisement (quảng cáo)
• Promotion (khuyến mãi)
• Brand awareness (nhận diện thương hiệu)

Phương pháp học từ vựng hiệu quả

1. Phương pháp ghi nhớ

Các kỹ thuật ghi nhớ từ vựng:

1. Sử dụng flashcards
2. Tạo mind map (sơ đồ tư duy)
3. Học theo cụm từ
4. Thực hành viết câu
5. Nghe và nhắc lại

2. Ứng dụng công nghệ

Các công cụ học tập hiện đại:

• Ứng dụng học từ vựng
• Podcast tiếng Anh
• Video học tiếng Anh
• Phần mềm quản lý từ vựng

Chiến lược ôn tập và củng cố

1. Lịch trình học tập

Xây dựng kế hoạch học:

• Học 20-30 từ mới mỗi ngày
• Ôn tập từ đã học sau 24 giờ
• Kiểm tra định kỳ hàng tuần
• Thực hành trong ngữ cảnh thực tế

2. Phương pháp kiểm tra

Các cách đánh giá tiến bộ:

1. Làm bài test từ vựng
2. Viết đoạn văn sử dụng từ mới
3. Nói chuyện với người bản ngữ
4. Tham gia các nhóm học tập

Tài nguyên học tập

1. Nguồn học liệu

Các nguồn tài liệu hữu ích:

• Sách luyện thi TOEIC
• Website học tiếng Anh
• Khóa học trực tuyến
• Tài liệu từ geographyconference.com

2. Hội thảo và khóa học

Hội Nghị Khoa Học Địa Lý Việt Nam (geographyconference.com) thường xuyên tổ chức:

• Hội thảo về phương pháp học TOEIC
• Khóa học từ vựng chuyên sâu
• Workshop luyện thi TOEIC
  Liên hệ:
• Hotline: 0915 15 15 15
• Email: [email protected]

Ứng dụng thực tế

1. Trong công việc

Cách áp dụng từ vựng vào công việc:

• Viết email chuyên nghiệp
• Tham gia họp bằng tiếng Anh
• Thuyết trình trong môi trường quốc tế
• Giao tiếp với đối tác nước ngoài

2. Trong giao tiếp hàng ngày

Sử dụng từ vựng trong:

• Trò chuyện casual
• Đọc tin tức tiếng Anh
• Xem phim, nghe nhạc
• Du lịch nước ngoài

Các lỗi thường gặp và cách khắc phục

1. Lỗi phát âm

Cách cải thiện phát âm:

• Nghe và bắt chước người bản ngữ
• Sử dụng từ điển phát âm
• Ghi âm và tự đánh giá
• Tham gia các lớp phát âm

2. Lỗi sử dụng

Tránh các lỗi phổ biến:

• Dùng sai ngữ cảnh
• Nhầm lẫn từ đồng âm
• Sai collocations
• Dùng từ không phù hợp văn phong

Đánh giá và theo dõi tiến bộ

1. Đặt mục tiêu

Xác định mục tiêu rõ ràng:

• Số lượng từ cần học
• Thời gian hoàn thành
• Điểm TOEIC mong muốn
• Khả năng ứng dụng thực tế

2. Theo dõi tiến độ

Phương pháp theo dõi:

1. Sử dụng ứng dụng quản lý học tập
2. Ghi chép nhật ký học tập
3. Đánh giá định kỳ
4. Điều chỉnh phương pháp học

Kết luận

Học từ vựng TOEIC theo chủ đề là một phương pháp hiệu quả để cải thiện khả năng tiếng Anh và đạt điểm cao trong kỳ thi. Việc kết hợp các phương pháp học tập, ứng dụng công nghệ và tham gia các khóa học tại geographyconference.com sẽ giúp bạn đạt được mục tiêu nhanh chóng.

Lời khuyên cuối cùng

Để thành công trong việc học từ vựng TOEIC:

1. Duy trì tính kỷ luật trong học tập
2. Thực hành thường xuyên
3. Tham gia cộng đồng học tập
4. Không ngừng cập nhật kiến thức mới

Hãy bắt đầu hành trình học từ vựng TOEIC của bạn ngay hôm nay và đừng quên tham khảo các khóa học chất lượng tại geographyconference.com để được hỗ trợ tốt nhất trên con đường chinh phục TOEIC!